Distributed Array

This example shows how to use the pylops_mpi.DistributedArray. This class provides a way to distribute arrays across multiple processes in a parallel computing environment.

from matplotlib import pyplot as plt
import numpy as np
from mpi4py import MPI

from pylops_mpi.DistributedArray import local_split, Partition
import pylops_mpi

plt.close("all")
np.random.seed(42)

# MPI parameters
size = MPI.COMM_WORLD.Get_size()  # number of nodes
rank = MPI.COMM_WORLD.Get_rank()  # rank of current node


# Defining the global shape of the distributed array
global_shape = (10, 5)

Let’s start by defining the class with the input parameters global_shape, partition, and axis. Here’s an example implementation of the class with axis=0.

arr = pylops_mpi.DistributedArray(global_shape=global_shape,
                                  partition=pylops_mpi.Partition.SCATTER,
                                  axis=0)
# Filling the local arrays
arr[:] = np.arange(arr.local_shape[0] * arr.local_shape[1] * arr.rank,
                   arr.local_shape[0] * arr.local_shape[1] * (arr.rank + 1)).reshape(arr.local_shape)
pylops_mpi.plot_distributed_array(arr)

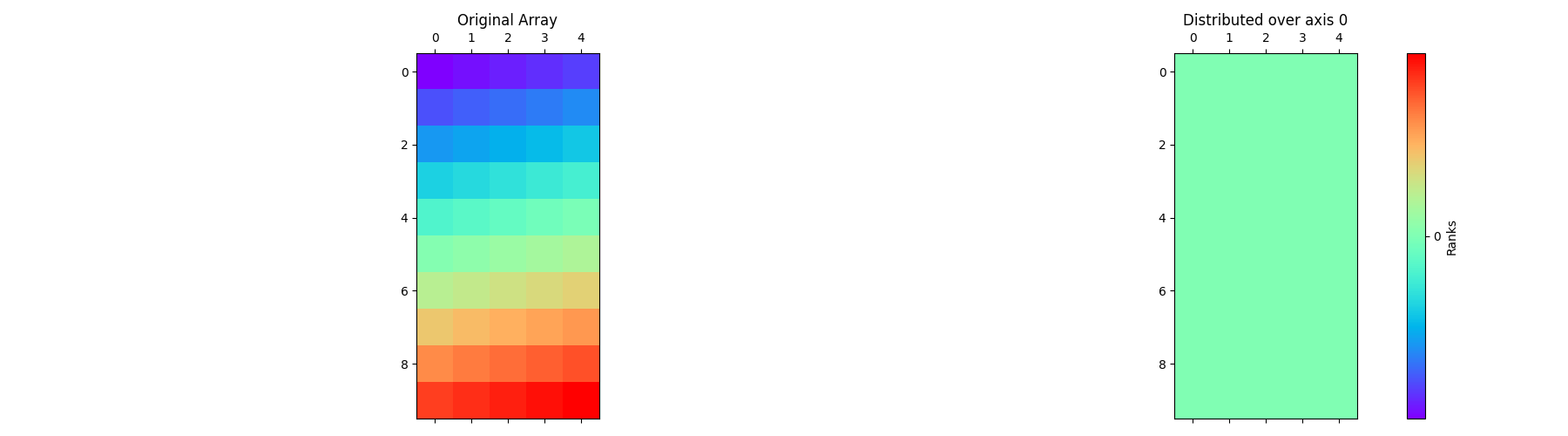
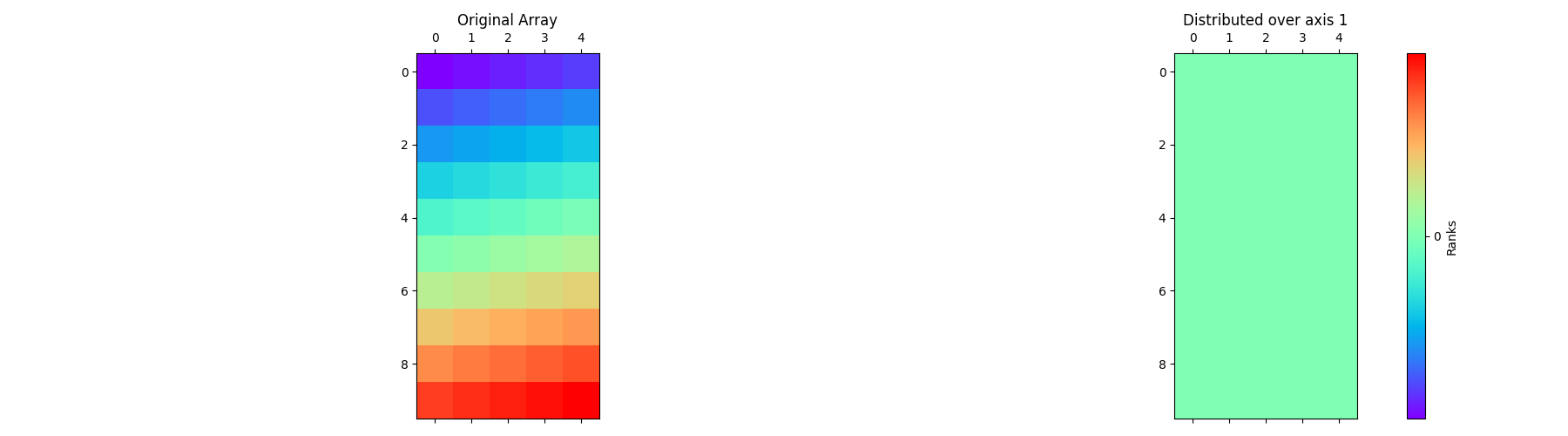
Below is an implementation to show how the global array is distributed along the second axis.

arr = pylops_mpi.DistributedArray(global_shape=global_shape,
                                  partition=pylops_mpi.Partition.SCATTER,
                                  axis=1)
# Filling the local arrays
arr[:] = np.arange(arr.local_shape[0] * arr.local_shape[1] * arr.rank,
                   arr.local_shape[0] * arr.local_shape[1] * (arr.rank + 1)).reshape(arr.local_shape)
pylops_mpi.plot_distributed_array(arr)

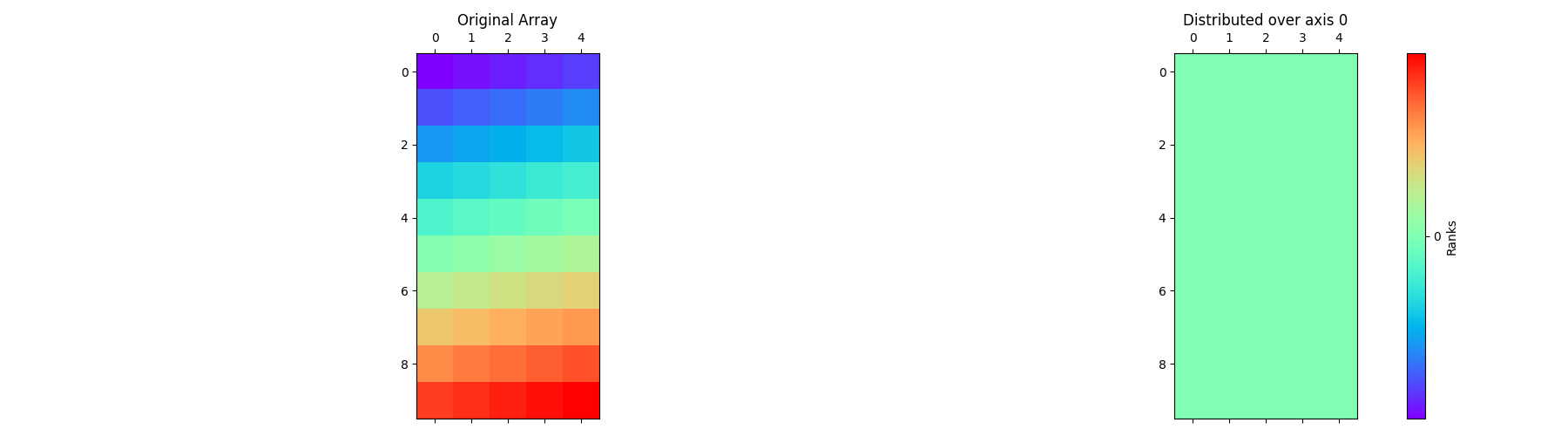
You also have the option of directly including the local_shapes as a parameter to the pylops_mpi.DistributedArray. This will enable the assignment of shapes to local arrays on each rank. However, it’s essential to ensure that the number of processes matches the length of local_shapes, and that the combined local shapes should align with the global_shape along the desired axis.

local_shape = local_split(global_shape, MPI.COMM_WORLD, Partition.SCATTER, 0)
# Assigning local_shapes(List of tuples)
local_shapes = MPI.COMM_WORLD.allgather(local_shape)
arr = pylops_mpi.DistributedArray(global_shape=global_shape, local_shapes=local_shapes, axis=0)
arr[:] = np.arange(arr.local_shape[0] * arr.local_shape[1] * arr.rank,
                   arr.local_shape[0] * arr.local_shape[1] * (arr.rank + 1)).reshape(arr.local_shape)
pylops_mpi.plot_distributed_array(arr)

To convert a random NumPy array into a pylops_mpi.DistributedArray, you can use the to_dist classmethod. This method allows you to distribute the array across multiple processes for parallel computation. Below is an example implementation depicting the same.

n = global_shape[0] * global_shape[1]
# Array to be distributed
array = np.arange(n) / float(n)
arr1 = pylops_mpi.DistributedArray.to_dist(x=array.reshape(global_shape), axis=1)
array = array / 2.0
arr2 = pylops_mpi.DistributedArray.to_dist(x=array.reshape(global_shape), axis=1)
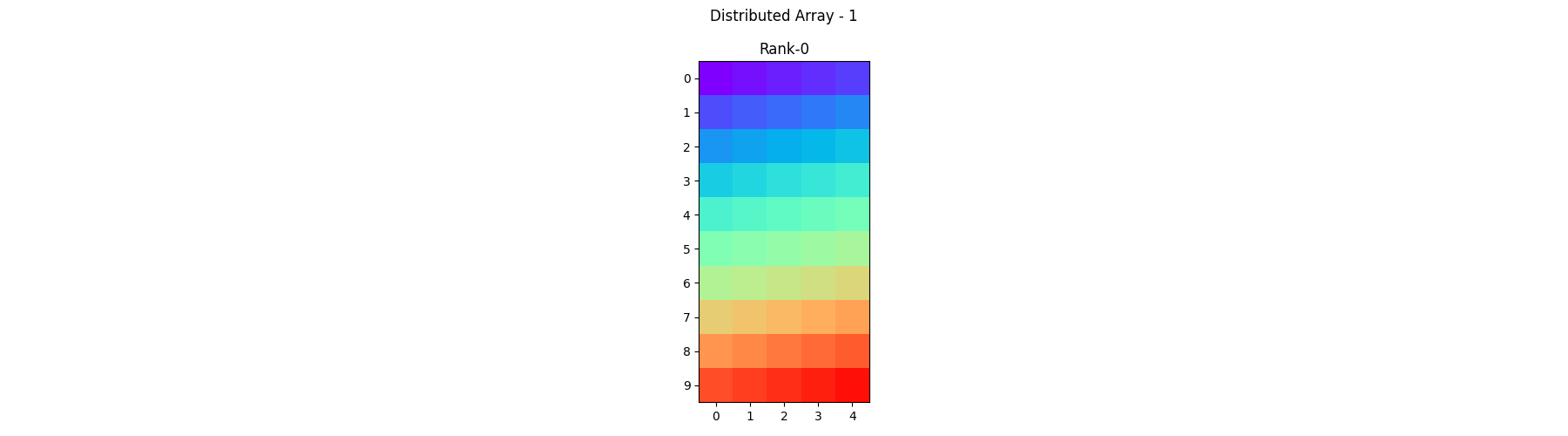
# plot local arrays
pylops_mpi.plot_local_arrays(arr1, "Distributed Array - 1", vmin=0, vmax=1)
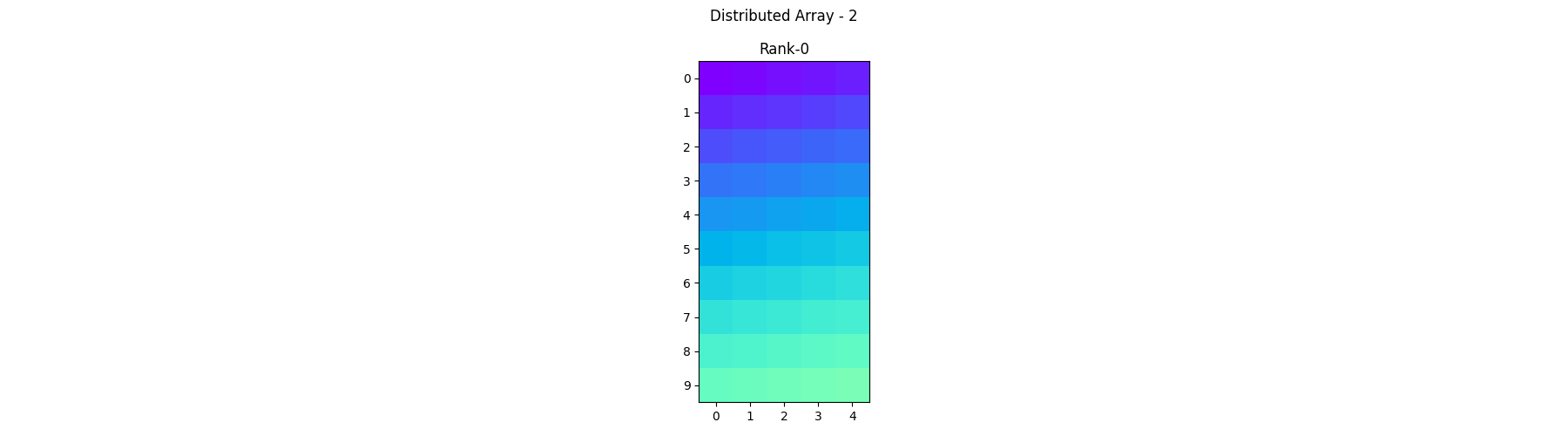
pylops_mpi.plot_local_arrays(arr2, "Distributed Array - 2", vmin=0, vmax=1)

• 
• 

Let’s move now to consider various operations that one can perform on pylops_mpi.DistributedArray objects.

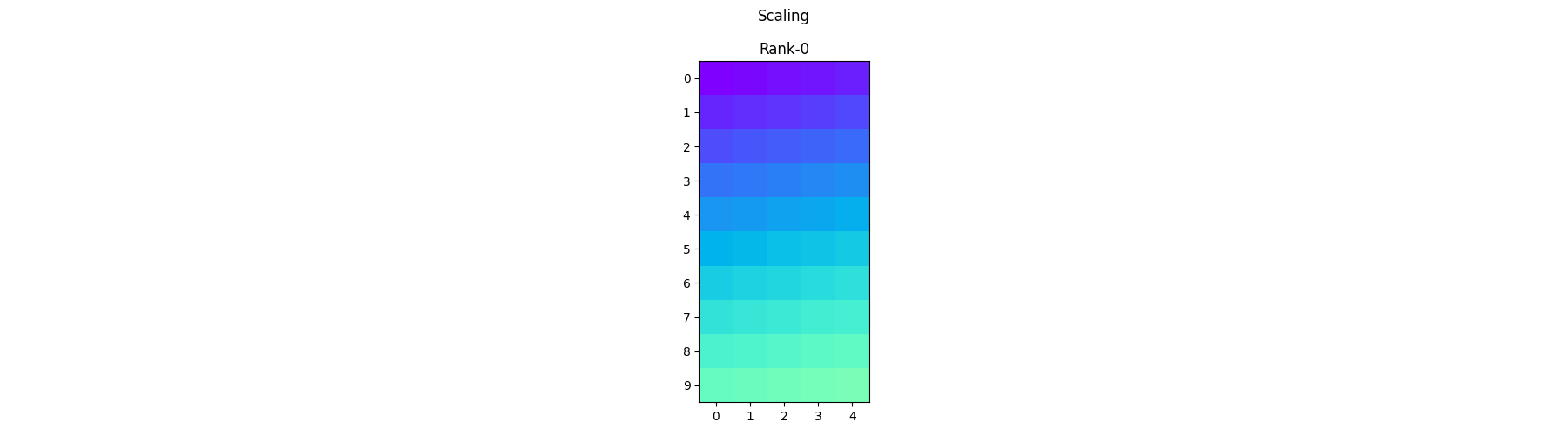
Scaling - Each process operates on its local portion of the array and scales the corresponding elements by a given scalar.

scale_arr = .5 * arr1
pylops_mpi.plot_local_arrays(scale_arr, "Scaling", vmin=0, vmax=1)

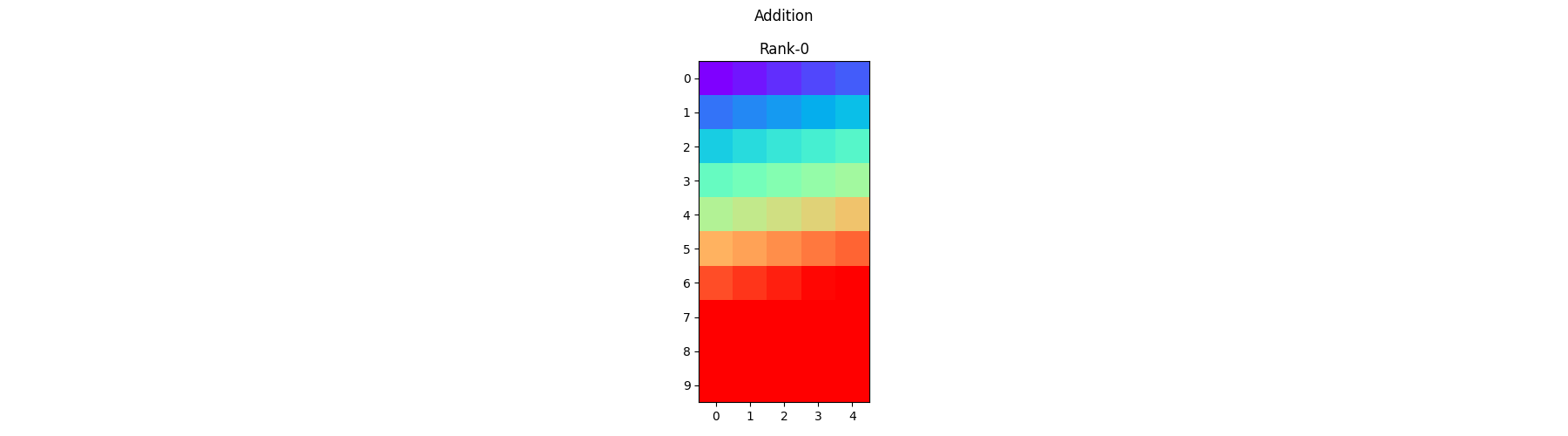
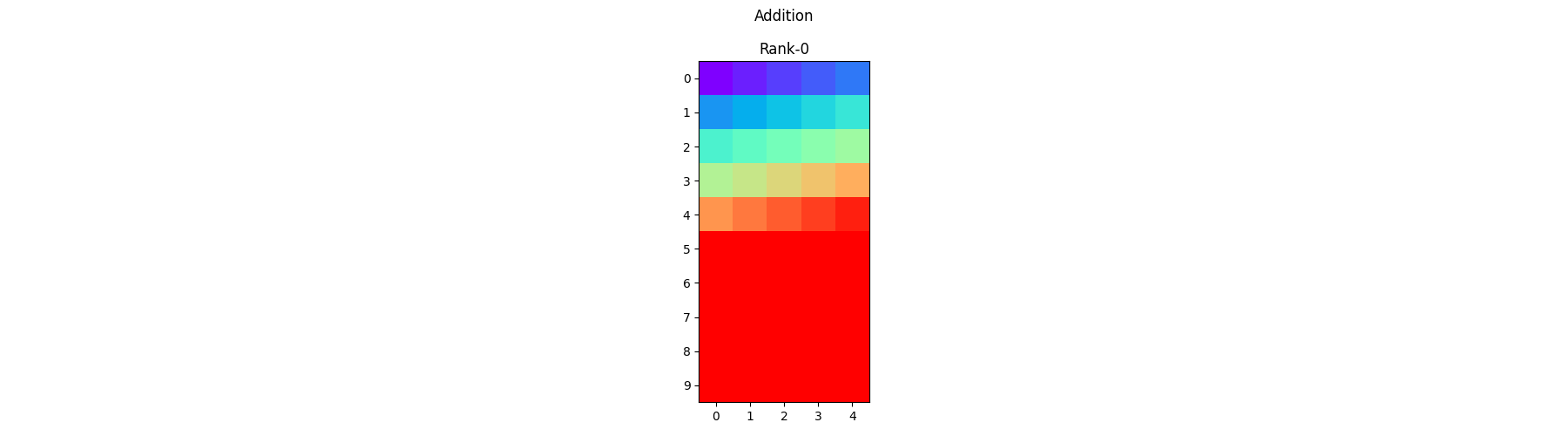
Element-wise Addition - Each process operates on its local portion of the array and adds the corresponding elements together.

sum_arr = arr1 + arr2
pylops_mpi.plot_local_arrays(sum_arr, "Addition", vmin=0, vmax=1)

Element-wise In-place Addition - Similar to the previous one but the addition is performed directly on one of the addends without creating a new distributed array.

sum_arr += arr2
pylops_mpi.plot_local_arrays(sum_arr, "Addition", vmin=0, vmax=1)

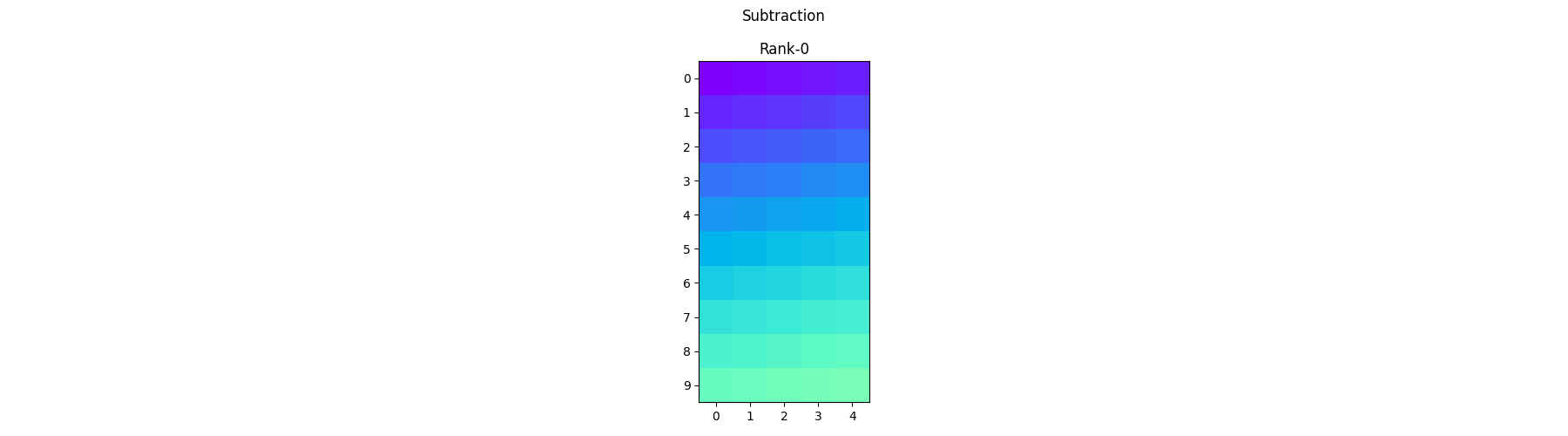
Element-wise Subtraction - Each process operates on its local portion of the array and subtracts the corresponding elements together.

diff_arr = arr1 - arr2
pylops_mpi.plot_local_arrays(diff_arr, "Subtraction", vmin=0, vmax=1)

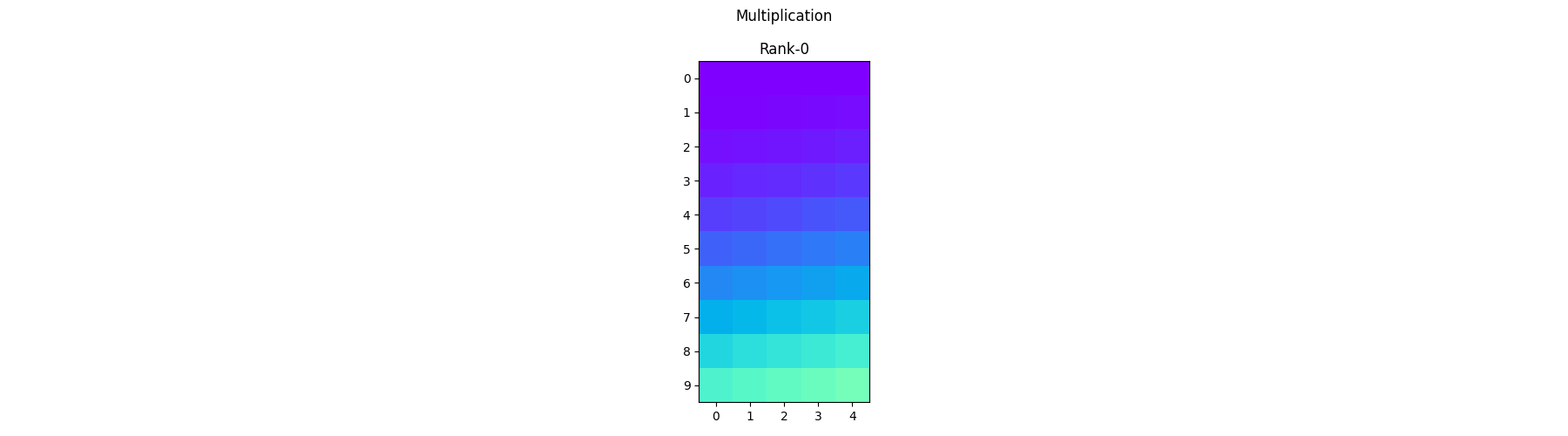
Element-wise Multiplication - Each process operates on its local portion of the array and multiplies the corresponding elements together.

mult_arr = arr1 * arr2
pylops_mpi.plot_local_arrays(mult_arr, "Multiplication", vmin=0, vmax=1)

Finally, let’s look at the case where parallelism could be applied over multiple axes - and more specifically one belonging to the model/data and one to the operator. This kind of “2D”-parallelism requires repeating parts of the model/data over groups of ranks. However, when global operations such as dot or norm are applied on a pylops_mpi.DistributedArray of this kind, we need to ensure that the repeated portions to do all contribute to the computation. This can be achieved via the mask input parameter: a list of size equal to the number of ranks, whose elements contain the index of the subgroup/subcommunicator (with partial arrays in different groups are identical to each other).

# Defining the local and global shape of the distributed array
local_shape = 5
global_shape = local_shape * size

# Create mask
nsub = 2
subsize = max(1, size // nsub)
mask = np.repeat(np.arange(size // subsize), subsize)
if rank == 0:
    print("1D masked arrays")
    print(f"Mask: {mask}")

# Create and fill the distributed array
x = pylops_mpi.DistributedArray(global_shape=global_shape,
                                partition=Partition.SCATTER,
                                mask=mask)
x[:] = (MPI.COMM_WORLD.Get_rank() % subsize + 1.) * np.ones(local_shape)
xloc = x.asarray()

# Dot product
dot = x.dot(x)
dotloc = np.dot(xloc[local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)],
                xloc[local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)])
print(f"Dot check (Rank {rank}): {np.allclose(dot, dotloc)}")

# Norm
norm = x.norm(ord=2)
normloc = np.linalg.norm(xloc[local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)],
                         ord=2)
print(f"Norm check (Rank {rank}): {np.allclose(norm, normloc)}")

1D masked arrays
Mask: [0]
Dot check (Rank 0): True
Norm check (Rank 0): True

And with 2d-arrays distributed over axis=1

extra_dim_shape = 2
if rank == 0:
    print("2D masked arrays (over axis=1)")

# Create and fill the distributed array
x = pylops_mpi.DistributedArray(global_shape=(extra_dim_shape, global_shape),
                                partition=Partition.SCATTER,
                                axis=1, mask=mask)
x[:] = (MPI.COMM_WORLD.Get_rank() % subsize + 1.) * np.ones((extra_dim_shape, local_shape))
xloc = x.asarray()

# Dot product
dot = x.dot(x)
dotloc = np.dot(xloc[:, local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)].ravel(),
                xloc[:, local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)].ravel())
print(f"Dot check (Rank {rank}): {np.allclose(dot, dotloc)}")

# Norm
norm = x.norm(ord=2, axis=1)
normloc = np.linalg.norm(xloc[:, local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)],
                         ord=2, axis=1)
print(f"Norm check (Rank {rank}): {np.allclose(norm, normloc)}")

2D masked arrays (over axis=1)
Dot check (Rank 0): True
Norm check (Rank 0): True

And finally with 2d-arrays distributed over axis=0

if rank == 0:
    print("2D masked arrays (over axis=0)")

# Create and fill the distributed array
x = pylops_mpi.DistributedArray(global_shape=(global_shape, extra_dim_shape),
                                partition=Partition.SCATTER,
                                axis=0, mask=mask)
x[:] = (MPI.COMM_WORLD.Get_rank() % subsize + 1.) * np.ones((local_shape, extra_dim_shape))
xloc = x.asarray()

# Dot product
dot = x.dot(x)
dotloc = np.dot(xloc[local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)].ravel(),
                xloc[local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)].ravel())
print(f"Dot check (Rank {rank}): {np.allclose(dot, dotloc)}")

# Norm
norm = x.norm(ord=2, axis=0)
normloc = np.linalg.norm(xloc[local_shape * subsize * (rank // subsize):local_shape * subsize * (rank // subsize + 1)],
                         ord=2, axis=0)
print(f"Norm check (Rank {rank}): {np.allclose(norm, normloc)}")

2D masked arrays (over axis=0)
Dot check (Rank 0): True
Norm check (Rank 0): True