CGLS Solver

This example demonstrates the utilization of pylops_mpi.optimization.basic.cgls solver. Our solver uses the pylops_mpi.DistributedArray to reduce the following cost function in a distributed fashion :

\[J = \| \mathbf{y} - \mathbf{Ax} \|_2^2 + \epsilon \| \mathbf{x} \|_2^2\]

import numpy as np
from mpi4py import MPI
from matplotlib import pyplot as plt

import pylops

import pylops_mpi

np.random.seed(42)
plt.close("all")
rank = MPI.COMM_WORLD.Get_rank()
size = MPI.COMM_WORLD.Get_size()

Let’s define a matrix with dimensions N and M and populate it with random numbers. Then, we will input this matrix in a pylops_mpi.basicoperators.MPIBlockDiag.

N, M = 20, 15
Mop = pylops.MatrixMult(A=np.random.normal(0, 1, (N, M)))
BDiag = pylops_mpi.MPIBlockDiag(ops=[Mop, ], dtype=np.float128)

By applying the pylops_mpi.basicoperators.MPIBlockDiag operator, we perform distributed matrix-vector multiplication.

x = pylops_mpi.DistributedArray(size * M, dtype=np.float128)
x[:] = np.ones(M)
y = BDiag @ x

We now utilize the cgls solver to obtain the inverse of the MPIBlockDiag. In the case of MPIBlockDiag, each operator is responsible for performing an inversion operation iteratively at a specific rank. The resulting inversions are then obtained in a pylops_mpi.DistributedArray. To obtain the overall inversion of the entire MPIBlockDiag, you can utilize the asarray() function of the DistributedArray as shown below.

# Set initial guess `x0` to zeroes
x0 = pylops_mpi.DistributedArray(BDiag.shape[1], dtype=np.float128)
x0[:] = 0
xinv, istop, niter, r1norm, r2norm, cost = pylops_mpi.cgls(BDiag, y, x0=x0, niter=15, tol=1e-10, show=True)
xinv_array = xinv.asarray()

if rank == 0:
    print(f"CGLS Solution xinv={xinv_array}")
    # Visualize
    plt.figure(figsize=(18, 5))
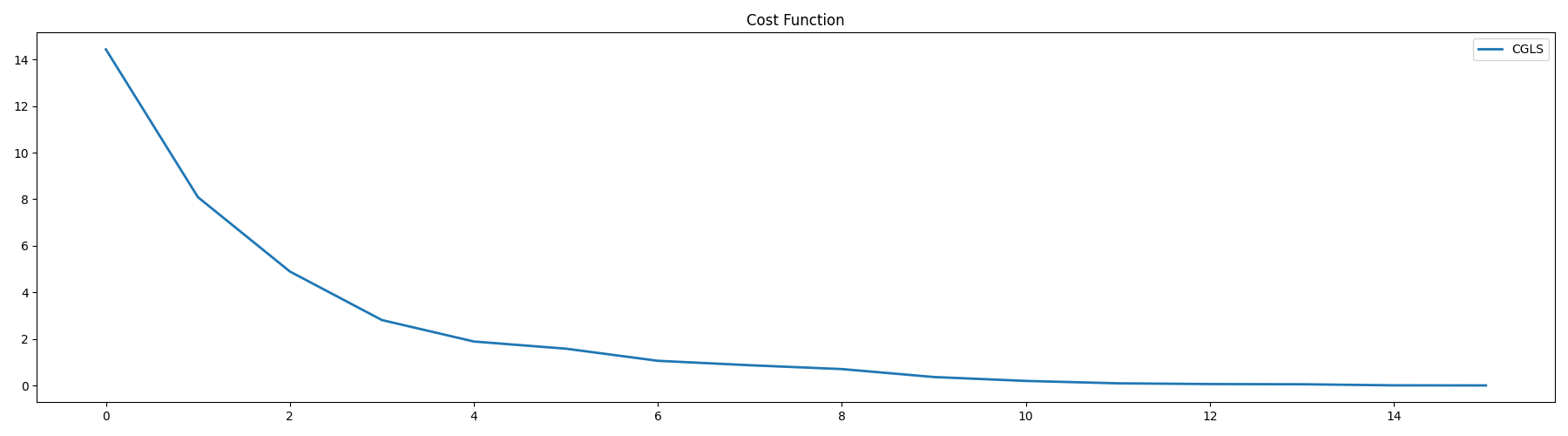
    plt.plot(cost, lw=2, label="CGLS")
    plt.title("Cost Function")
    plt.legend()
    plt.tight_layout()

CGLS
-----------------------------------------------------------------
The Operator Op has 20 rows and 15 cols
damp = 0.000000e+00     tol = 1.000000e-10      niter = 15
-----------------------------------------------------------------

    Itn          x[0]              r1norm         r2norm
     1        2.7357e-01         8.0894e+00     8.0894e+00
     2        4.5467e-01         4.8937e+00     4.8937e+00
     3        9.5671e-01         2.8091e+00     2.8091e+00
     4        1.0115e+00         1.8866e+00     1.8866e+00
     5        9.8370e-01         1.5786e+00     1.5786e+00
     6        8.9488e-01         1.0577e+00     1.0577e+00
     7        8.9476e-01         8.6760e-01     8.6760e-01
     8        9.2004e-01         7.0216e-01     7.0216e-01
     9        1.0346e+00         3.6129e-01     3.6129e-01
    10        1.0465e+00         1.9343e-01     1.9343e-01
    11        1.0186e+00         9.0684e-02     9.0684e-02
    12        1.0133e+00         5.8939e-02     5.8939e-02
    13        1.0095e+00         5.0127e-02     5.0127e-02
    14        9.9946e-01         3.9693e-03     3.9693e-03
    15        1.0000e+00         3.7502e-07     3.7502e-07

Iterations = 15        Total time (s) = 0.03
-----------------------------------------------------------------

CGLS Solution xinv=[0.99999999 1.00000001 0.99999999 0.99999999 1.00000002 1.
 1.         0.99999999 0.99999999 1.         1.         1.
 0.99999999 1.         0.99999996]